힙 정렬(Heap Sort)은 큌 정렬(Quick sort)과 병합 정렬(Merge Sort)과 같은 시간 복잡도 O(N*logN)를 가지고 있다.
힙 트리를 이용하는 정렬 방법이다.
힙 트리란

힙 트리의 조건 중 부모 노드의 값은 항상 자식 노드(하위 노드)의 값보다 크거나 작아야 한다.
힙 트리는 위의 조건은 만족하는 정렬은 두가지 뿐이다. 최대 힙(Max Heap), 최소 힙(Min Heap)

힙 트리 구조의 자녀 트리 사이에는 대소관계는 정해지지 않는다.
또한 힙 트리는 완전 이진 트리를 조건으로 가지고 있어야 한다.
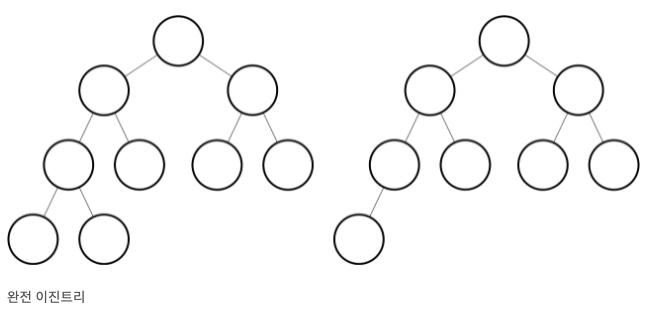
왼쪽부터 차근차근 채워나가며 1~n까지 만들어지는 트리구조이다.
완전 이진 트리의 장점은 트리를 배열로 쉽게 구현이 가능하며, 부모 노드와 자식 노드 간에 관계를 수식화 할 수 있다.
노드에 있는 값을 index 값으로 가정하면


- 부모 노드 index 값 - 자식 노드 index 값 / 2
- 왼쪽 자식 노드 index 값 - 부모 노드 index* 2
- 오른쪽 자식 노드 index 값 - 부모 노드 index * 2 + 1
으로 나타난다.
(참고 - 트리와 이진 트리(Binary Tree))
힙 트리를 생성 할때 사용하는 알고리즘 Heapify Algorithm
Heapify Algorithm 은 부모 노드의 두 자식 중 더 큰 자식과 자신의 위치를 바꾸는 알고리즘으로 바텀 업 (Bottom up) 또는 탑 다운(Top down) 방식으로 정렬해 나간다.
힙 정렬
힙 정렬(Heap sort)은 힙 생성 알고리즘(Heapify Agorithm)을 사용하여 정렬된 힙 트리(Heap Tree) 구조를 이용하는 것이다.
힙 트리 구조가 있으면 최대 힙(Max heap) 혹은 최소 힙(Min heap)으로 정렬되어 있을 것이다.
최상위 노드를 마지막 노드로 바꿔주는 과정을 반복하면 힙 정렬이 된다.
예를 들어 최대 힙을 가지고 오름 차순을 한다고 가정하면
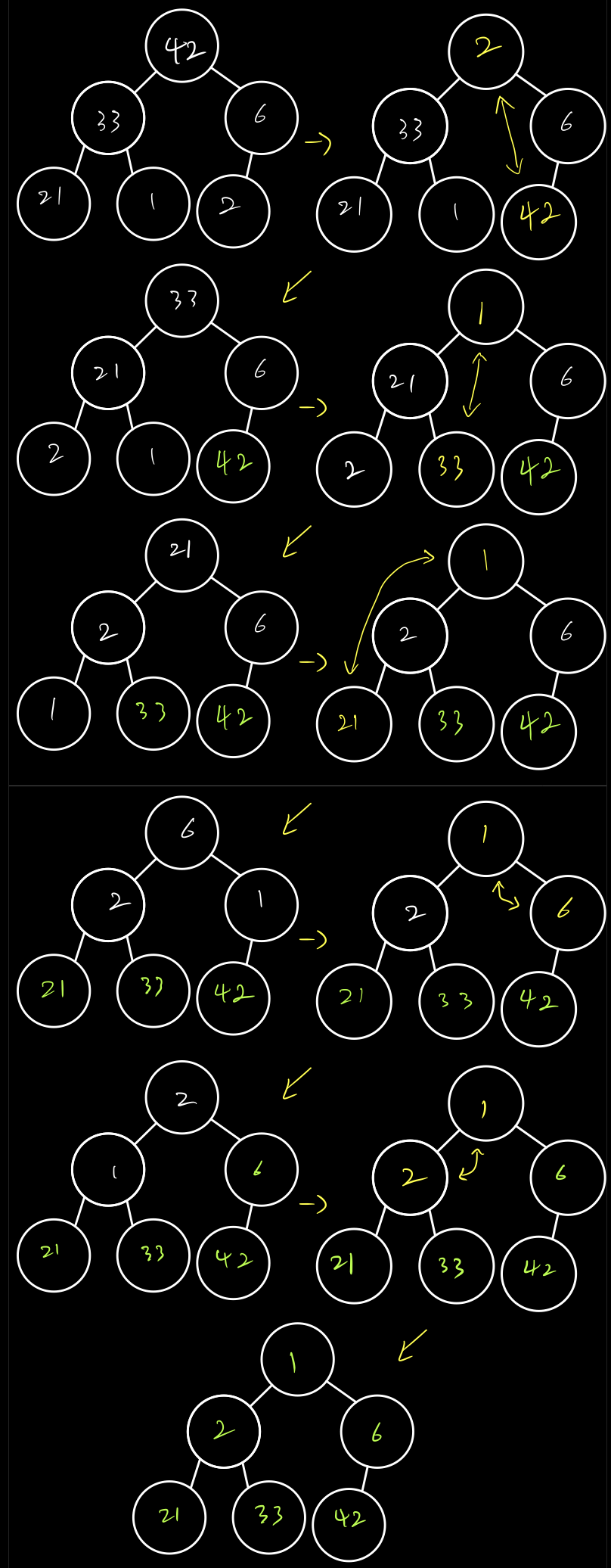
힙 트리 생성 알고리즘의 시간 복잡도는 O(N logN)
힙 트리 생성하는 방법엔 2가지가 있다.
삽입하면서 heapify O(N logN)
완전 이진트리를 heapify O(N)
(설명 좋은 블로그 - ratsgo.github.io/data%20structure&algorithm/2017/09/27/heapsort/)
힙 트리 생성 알고리즘 O(N)
전체 원소의 개수 (N) * 트리의 높이 (logN)
즉, 힙 정렬의 전체 시간 복잡도는 O(N) + O(N logN) -> O(N logN)이 된다.
C언어 - 힙 정렬 구현 코드
#include #define num 8 int node[] = {2,1,33,21,6,42,50,5}; void heapify(int n, int start, int *node) { int l,r,tmp; l = start*2+1; r = start*2+2; if(r>n) { return; } if(node[l] > node[start] || node..
iyk2h.tistory.com
'CS > 알고리즘 및 자료구조' 카테고리의 다른 글
| C언어 - 힙 정렬 구현 코드 (0) | 2021.05.21 |
|---|---|
| 하이퍼밴드(Hyperband), Successive Halving Algorithm(SHA)의 흐름 이해하기 (0) | 2021.05.19 |
| c언어 - 이진 트리 레벨 순회 (LevelTraverse) (1) | 2021.04.16 |
| C언어 - 큐, 큐 구현 (Queue), 배열 구현 (0) | 2021.03.12 |
| C언어 - 이진 트리, 이진 탐색 트리 구현 (binary tree, binary search tree) (0) | 2021.03.05 |



댓글